Assignment 3 – Term and type-level recursion

The GitHub Classrooms link for this assignment is here

The deadline for the assignment is 2024-03-10 @ 23:59. The deadline for the peer reviews is 2022-03-17 @ 23:59.

Exercise 1 – Term-level fixpoints (2 pts)

Given the function
```
 fix :: (a -> a) -> a
 fix f = f (fix f)
```
Define the function foldr as an application of fix to a term that is not recursive.
The lambda term which corresponds to the Y-combinator in untyped lambda calculus
```
 y = \f -> (\x -> f (x x)) (\x -> f (x x))
```
does not type check in Haskell. Try it and explain the error message you get.

Interestingly though, recursion on the type level can be used to introduce recursion on the value level. If we define the recursive type:
```
 data F a = F { unF :: F a -> a }
```
then we can “annotate” the definition of y with applications of F and unF such that y typechecks. Do it!

NOTE: Attempting to optimise this function will cause GHC’s simplifier to diverge. Sometimes you can avoid this by adding {-# OPTIONS_GHC -fmax-simplifier-iterations=1 #-} to the top of the file.

Exercise 2 – Nested types (4 pts)

Here is a nested data type for square matrices:

type Square      = Square' Nil  -- note that it is eta-reduced
data Square' t a = Zero (t (t a)) | Succ (Square' (Cons t) a)

data Nil    a = Nil
data Cons t a = Cons a (t a)

Question 1. Give Haskell code that represents the following two square matrices as elements of the Square data type:

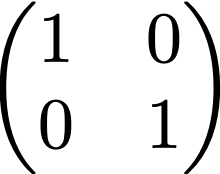
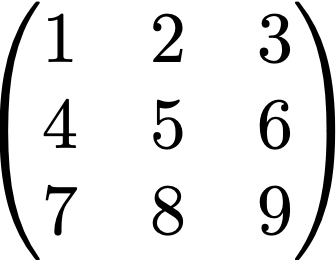
Let’s investigate how we can derive an equality function on square matrices. We do so very systematically by deriving an equality function for each of the four types. We follow a simple, yet powerful principle: type abstraction corresponds to term abstraction, and type application corresponds to term application.

What does this mean? If a type f is parameterized over an argument a, then in general, we have to know how equality is defined on a in order to define equality on f a. Therefore we define

eqNil :: (a -> a -> Bool) -> (Nil a -> Nil a -> Bool)
eqNil eqA Nil Nil = True

In this case, the a is not used in the definition of Nil , so it is not surprising that we do not use eqA in the definition of eqNil. But what about Cons? The data type Cons has two arguments t and a, so we expect two arguments to be passed to eqCons, something like

eqCons eqT eqA (Cons x xs) (Cons y ys) = eqA x y && ...

But what should the type of eqT be? The t is of kind * -> *, so it can’t be t -> t -> Bool. We can argue that we should use t a -> t a -> Bool, because we use t applied to a in the definition of Cons. However, a better solution is to recognise that, being a type constructor of kind * -> *, an equality function on t should take an equality function on its argument as a parameter. And, moreover, it does not matter what this parameter is! A function like eqNil is polymorphic in type a, so let us require that eqT is polymorphic in the argument type as well:

eqCons :: (forall b . (b -> b -> Bool) -> (t b -> t b -> Bool))
       -> (a -> a -> Bool)
       -> (Cons t a -> Cons t a -> Bool)
eqCons eqT eqA (Cons x xs) (Cons y ys) = eqA x y && eqT eqA xs ys

Now you can see how we apply eqT to eqA when we want equality at type t a – the type application corresponds to term application.

Question 2. A type with a forall on the inside requires the extension RankNTypes to be enabled. Try to understand what the difference is between a function of the type of eqCons and a function with the same type but the forall omitted. Can you omit the forall in the case of eqCons and does the function still work?

Now, on to Square'. The type of eqSquare' follows exactly the same idea as the type of eqCons:

eqSquare' :: (forall b . (b -> b -> Bool) -> (t b -> t b -> Bool))
          -> (a -> a -> Bool)
          -> (Square' t a -> Square' t a -> Bool)

We now for the first time have more than one constructor, so we actually have to give multiple cases. Let us first consider comparing two applications of Zero:

eqSquare' eqT eqA (Zero xs) (Zero ys) = eqT (eqT eqA) xs ys

Note how again the structure of the definition follows the structure of the type. We have a value of type t (t a). We compare it using eqT, passing it an equality function for values of type t a. How? By using eqT eqA. The remaining cases are as follows:

eqSquare' eqT eqA (Succ xs) (Succ ys) = eqSquare' (eqCons eqT) eqA xs ys
eqSquare' eqT eqA _         _         = False

The idea is the same – let the structure of the recursive calls follow the structure of the type.

Question 3. Again, try removing the forall from the type of eqSquare'. Does the function still type check? Try to explain!

Now we’re done:

eqSquare :: (a -> a -> Bool) -> Square a -> Square a -> Bool
eqSquare = eqSquare' eqNil

Test the function. We can now also give an Eq instance for Square – this requires the minor language extension TypeSynonymInstances, because Haskell 98 does not allow type synonyms like Square to be used in instance declarations:

instance Eq a => Eq (Square a) where
  (==) = eqSquare (==)

Question 4. Systematically follow the scheme just presented in order to define a Functor instance for square matrices. I.e., derive a function mapSquare such that you can define

instance Functor Square where
  fmap = mapSquare

This instance requires Square to be defined in eta-reduced form in the beginning, because Haskell does not allow partially applied type synonyms. If we had defined Square differently

type Square a = Square' Nil a

we cannot make Square an instance of the class Functor.

Question 5. Why is this restriction in place? Try to find problems arising from partially applied type synonyms, and describe them (as concisely as possible) with a few examples.

Exercise 3 – Teletype IO (4 pts)

Consider the following data type:

data Teletype a = End a
                | Get (Char -> Teletype a)
                | Put Char (Teletype a)

A value of type Teletype can be used to describe programs that read and write characters and return a final result of type a. Such a program can end immediately (End). If it reads a character, the rest of the program is described as a function depending on this character (Get). If the program writes a character (Put), the value to show and the rest of the program are recorded.

For example, the following expression describes a program that continuously echo characters:

echo = Get (\c -> Put c echo)

Question 1. Write a Teletype-program getLine which reads characters until it finds a newline character, and returns the complete string.

A map function for Teletype can be defined as follows:

instance Functor Teletype where
  fmap f (End x)   = End (f x)
  fmap f (Get g)   = Get (fmap f . g)
  fmap f (Put c x) = Put c (fmap f x)

Question 2. Define sensible Applicative and Monad instances for Teletype.

The definition of Teletype is not directly compatible with do notation. Usually, you have getChar and putChar primitives which allow you to write instead:

echo = do c <- getChar
          putChar c
          echo

Question 3. Define those functions getChar :: Teletype Char and putChar :: Char -> Teletype ().

Question 4. Define a MonadState instance for Teletype. How is the behavior of this instance different from the usual State type?

Question 5. A Teletype-program can be thought as a description of an interaction with the console. Write a function runConsole :: Teletype a -> IO a which runs a Teletype-program in the IO monad. A Get should read a character from the console and Put should write a character to the console.

One of the advantages of separating the description of Teletype-programs from their executions is that we can interpret them in different ways. For example, the communication might take place throught a network instead of console. Or we could mock user input and output for testing purposes.

Question 6. Write an interpretation of a Teletype-program into the monad RWS [Char] () [Char] (documentation). In other words, write a function,

type TeletypeRW = RWS [Char] () [Char]
runRWS :: Teletype a -> TeletypeRW a

Using it, write a function mockConsole :: Teletype a -> [Char] -> (a, [Char]).