SIMULATION ASSIGNMENT THE UITHOFLIJN: Information

(from www.uithoflijn.nl)
Research questions
In this simulation study, we will consider the Uithoflijn, the new tram line between the central station of Utrecht and de Uithof which will start operating in the future. (see also www.uithoflijn.nl. We will study the operational performance of this line. You have to answer the following questions:
- What are feasible frequencies for the Uithoflijn?
- Which turn-around should be used at the end points?
- U-ov plans to use a frequency of 16 trams per hour. How well does this frequency handle the amount of passengers from the prognosis? How much passenger growth can be handled with this frequency?
Performance measures
Important performance measures are:
- Punctuality: this is computed from the departure delays at the end stations (CS and P+R). The departure delay of a tram is the difference between the actual departure time and the departure time in the timetable. To measure the punctuality we use the percentage of trams with a departure delay of 1 minute or more. It is also recommended to measure the average departure delay and the maximum departure delay. You should distinguish the different end stations.
- Passenger waiting times
Problem description
Passenger model
You may assume that the passengers arrive at the stops according to a Poisson Process from which the rate varies over the day. This rate is determined per 15 minutes.
For the Uithoflijn, we do not have passenger counts, but we can predict them using the data for bus route 12 and the passenger prognosis from province of Utrecht. This information is enclosed in the set of data files.
When a tram arrives at a stop, first passengers exit the tram and after that passenger enter the tram.You may assume that passengers enter the tram in a FIFO order, i.e. passengers enter the tram in order of arrival time at the stop.
The capacity of the tram is 420 passengers. If the tram is full, passenger that want to enter wait for the next tram. Passengers that came to a stop to take the tram will never leave because of a long waiting time. The stops do not have capacity limits.
Driving times
The Uithoflijn consists of 7.9 km of track, with 9 stops. In the following tables, a list of all stops are given. In these tables, some more information is given. Because the tram follows more or less the same route as bus route 12, the corresponding stops are also given. In the last column of each table, the average driving time between each pair of stops is given. Note that this driving time is pure driving time, without the dwell time, where the dwell time is the time that a tram is standing still at the stop.
Driving times suffer from variation and should therefore be modelled as stochastic variables. We assume that the probability distribution can be based on the driving times from the SUNIj line (line to Nieuwegeid and Ijsselstein). These driving are available is the set of data files.
We assume that all variation is included in the stochastic model and do not model other disturbances during driving.
| Stop | Corr. stop route 12 | Distance(km) | Avg. Driving time(sec) |
|---|---|---|---|
| Centraal Station | CS Centrumzijde | ||
| Vaartsche Rijn | Bleekstraat | 1.4 | 134 |
| Galgenwaard | Galgenwaard | 3.1 | 243 |
| Kromme Rijn | De Kromme Rijn | 0.6 | 59 |
| Padualaan | Padualaan | 0.8 | 101 |
| Heidelberglaan | Heidelberglaan | 0.4 | 60 |
| UMC | AZU | 0.4 | 86 |
| WKZ | 0.6 | 78 | |
| P+R De Uithof | 0.6 | 113 |
| Stop | Corr. stop route 12 | Distance(km) | Avg. Driving time(sec) |
|---|---|---|---|
| P+R De Uithof | |||
| WKZ | 0.6 | 110 | |
| UMC | AZU | 0.6 | 78 |
| Heidelberglaan | Heidelberglaan | 0.4 | 82 |
| Padualaan | Padualaan | 0.4 | 60 |
| Kromme Rijn | De Kromme Rijn | 0.8 | 100 |
| Galgenwaard | Galgenwaard | 0.6 | 59 |
| Vaartsche Rijn | Bleekstraat | 3.1 | 243 |
| Centraal Station | CS Centrumzijde | 1.4 | 135 |
Timetable
Qbuzz (U-OV) works with a timetable for the departure at the end stations. At an end station, a tram will not depart before the departure time given in the timetable. This timetable is defined as follows. We first fix our frequency, suppose for example that this is 15 (trams per hour). We assume that the frequency is fixed during the complete day, i.e. from 6.00 to 21.30. Than we fix the departure times at P+R de Uithof as
- .00
- .04
- .08
- .12
- etc
- .02
- .06
- .10
- .14
- .18
- .22
- etc.
Stations: intermediate stops
At the intermediate stops there is a platform at each side of the tracks. A tram can not switch track but stops and leaves after the exit and entry of passengers is finished.
A tram can only enter an intermediate stop, when the previous tram in the same direction has left at least 40 second ago.
The time that a tram is standing still at the stop is called dwell time. The dwell time is modelled as a stochastic variable and depends on the number of passengers leaving and entering the tram. The average dwell time d is given by d = 12.5 + 0.22 p(in) + 0.13 p(out), where p(in) and p(out) are the number of passengers entering and leaving the tram, respectively. For the distribution of the dwell time, we use a gamma distribution with shape parameter k=2 and a minimum value of 0.8d. The tram dwells at every stop.
Stations: end points
The end point CS and P+R De Uithof have a special layout. At each end point there are two parallel tracks with a platform in between. At the end point, all passengers in the tram get out and at the same platform new passengers get in. In the mean time, to switch driving direction, the driver has to walk to the driver's cab at the other side of the tram. This is all included in the turn-around time. The timetable includes a planned turn-around time q. Technically, the minimum turn-around time is 3 minutes. When the tram arrives at the end station, it tries to depart at the time of the next `unexecuted' trip in the timetable. However, if the next `unexecuted' trip in the time table is within 3 minutes (so e.g. in 2 minutes), this would imply that the actual time for turn-around becomes shorter than 3 minutes. Since this is not allowed, the tram leaves after exactly 3 minutes.
Before the platform section there is a so-called `cross-switch' through which the trams can move to another track. We model the switch as a server with a processing time of one minute, a switch can process one tram at a time. There is one exception, two trams that do not cross can use the switch at the same time. Arriving trams have priority over departing trams. A schematic layout is given in Figure 1.
Note that here multiple interpretations are possible: 1) What we originally meant and happens in practice, is that a tram can only start crossing the switch after it has been empty for 1 minute, but crossing the switch itself takes hardly any time. 2) Another explanation that (understandably) has been chosen is that the tram physically occupies the switch for 1 minute. So crossing the switch takes 1 minute. (In the grading
both alternatives will be considered to be correct)
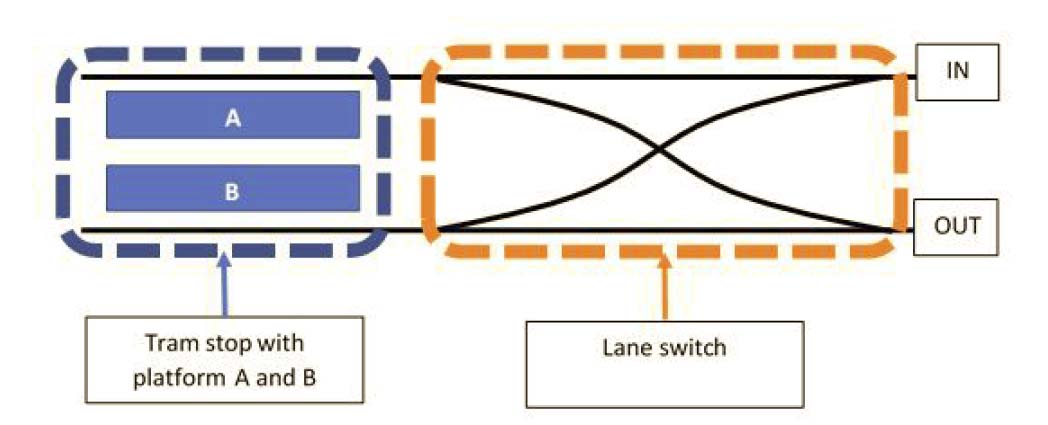
Figure 1: Layout end station.
Tram depot
During the night, trams are located at a depot which is connected to the P+R end station. The trams leave in the morning to start up the timetable and return in the evening after the timetable is finished. Trams are allowed to drive without passengers at the start or end of the days. Since the frequency is fixed over the day, trams do not move to and from the depot during the day. If there are delays during the day, this cannot be solved by taking additional trams from the depot.
Optional features
Additional research questions:- Introduce a dependency of the dwell time on the number of patients in the tram.
- Driver switch at CS: When a tram arrives a new driver is waiting at the platform to drive the tram in the other direction. This avoids the walking time of the driver and enables a shorter turn-around time. This is particularly interesting at a busy station, where the driver may get stuck in the crowd when walking to the other side of the tram. You may assume that after arrival of a tram, the driver needs 15 seconds to switch off equipment and get out. Also before departure, a driver needs 15 seconds to switch on equipment.
- Any other measure that seems fit to improve the performance
Data for the Simulation
You find files that contains data that you will need for the tram simulation through this link (you will get the password separately). These files contain:- Information about the number of passengers on the current bus route 12.
- Forecast for the number of passengers.
- A large set of runtime measurements from the Nieuwegein-tramline.
- Artificial input files for validation purposes